Curiousily

Data Imputation using Autoencoders | What to do when data is missing? (Part II)

02.02.2017 — Data Imputation, Neural Networks, Autoencoders, Python — 4 min read

Mushrooms, anyone? What if you have lots of data on mushrooms, yet some of it is missing? One important question you might want to answer is whether or not a particular specimen is edible or poisonous. Of course, your understanding of what a poisonous mushroom is might be quite different (hi to all from Netherlands), but I digress.

The dataset of interest will be (you guessed it) all about mushrooms. It describes physical characteristics of 8124 mushroom instances. The number of variables is 23, all of which are categorical. More information about the dataset can be found here.

1. Autoencoders

Which one do you like better?

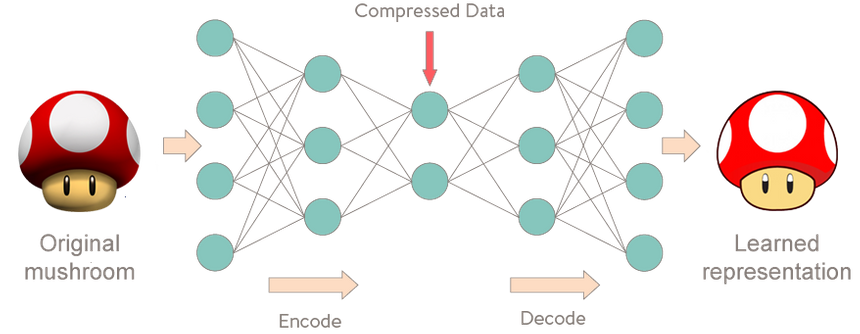
Strangely enough, an autoencoder is a model that given input data tries to predict it. It is used for unsupervised learning (That might not be entirely correct). Puzzling? First time I heard the concept I thought it must be a misunderstanding on my part. It wasn’t.

More specifically, let’s take a look at Autoencoder Neural Networks. This autoencoder tries to learn to approximate the following identity function:

\textstyle f_{W,b}(x) \approx x

While trying to do just that might sound trivial at first, it is important to note that we want to learn a compressed representation of the data, thus find structure. This can be done by limiting the number of hidden units in the model. Those kind of autoencoders are called undercomplete.

1.1 Choosing loss function

In order to learn something meaningful, autoencoders should try to minimize some function, called reconstruction error. The traditional squared error is often used:

\textstyle L(x,x') = ||\, x - x'||^2

2.1 Encoding the data

Our dataset contains categorical variables exclusively. We will use a standard approach for such cases - one-hot encoding. Furthermore, we have to handle cells with missing values. We will create a missing mask vector and append it to our one-hot encoded values. Missing values will be filled with some constant.

Let’s take a look at this sample data:

1[
2    ['blue stem', 'large cap'],
3    [None, 'large cap'],
4    ['green stem', None]
5]

Our encoded data looks like this:

1[
2    [1, 0, 0, 1, 0, 0, 0, 0, 0, 0], # no missing values
3    [0, 0, 1, 1, 0, 1, 1, 1, 0, 0], # missing value in 1st variable
4    [0, 1, 0, 0, 1, 0, 0, 0, 1, 1]  # missing value in 2nd variable
5]

2.2 Reconstruction error

Our reconstruction error will be the mean squared error which hopefully will work for categorical data. Since we are using Keras, our function must adhere to some rules.

1def make_reconstruction_loss(n_features):
2
3    def reconstruction_loss(input_and_mask, y_pred):
4        X_values = input_and_mask[:, :n_features]
5        X_values.name = "$X_values"
6
7        missing_mask = input_and_mask[:, n_features:]
8        missing_mask.name = "$missing_mask"
9        observed_mask = 1 - missing_mask
10        observed_mask.name = "$observed_mask"
11
12        X_values_observed = X_values * observed_mask
13        X_values_observed.name = "$X_values_observed"
14
15        pred_observed = y_pred * observed_mask
16        pred_observed.name = "$y_pred_observed"
17
18        return mse(y_true=X_values_observed, y_pred=pred_observed)
19    return reconstruction_loss

Additionally, we will use slightly modified mean squared error for assessing our progress during training. The function takes into account the mask of the input data:

1def masked_mae(X_true, X_pred, mask):
2    masked_diff = X_true[mask] - X_pred[mask]
3    return np.mean(np.abs(masked_diff))

2.3 Getting everything just right

Of course, a couple of imports are needed to make everything work. Make sure you have the proper libraries installed (all available via pip install).

1import random
2import pandas as pd
3import numpy as np
4import matplotlib.pylab as plt
5import seaborn as sns
6from keras.utils import np_utils
7from sklearn.preprocessing import LabelEncoder
8
9from keras.objectives import mse
10from keras.models import Sequential
11from keras.layers.core import Dropout, Dense
12from keras.regularizers import l1l2
13
14from collections import defaultdict

1%matplotlib inline

2.4 Creating the model (the fun part)

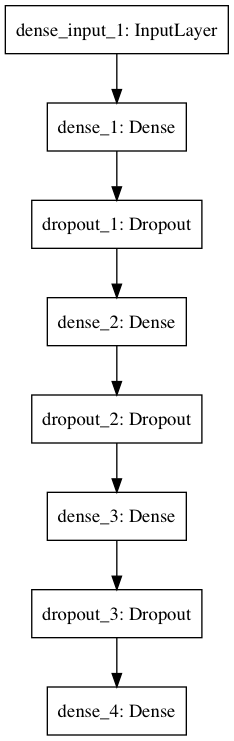
The following implementation is heavily based on the one provided by fancyimpute. Our NN has 3 hidden layers (with ReLU activation functions) with dropout probability set to 0.5. You can also choose two regularizers coefficients - the sum of the weights (L1) and sum the squares of the weights (L2). These are 0. The activation function for the output layer is sigmoid. It appears to work better than linear for our use case.

Here is the code for it, don’t be afraid to fiddle with it:

1class Autoencoder:
2
3    def __init__(self, data,
4                 recurrent_weight=0.5,
5                 optimizer="adam",
6                 dropout_probability=0.5,
7                 hidden_activation="relu",
8                 output_activation="sigmoid",
9                 init="glorot_normal",
10                 l1_penalty=0,
11                 l2_penalty=0):
12        self.data = data.copy()
13        self.recurrent_weight = recurrent_weight
14        self.optimizer = optimizer
15        self.dropout_probability = dropout_probability
16        self.hidden_activation = hidden_activation
17        self.output_activation = output_activation
18        self.init = init
19        self.l1_penalty = l1_penalty
20        self.l2_penalty = l2_penalty
21
22    def _get_hidden_layer_sizes(self):
23        n_dims = self.data.shape[1]
24        return [
25            min(2000, 8 * n_dims),
26            min(500, 2 * n_dims),
27            int(np.ceil(0.5 * n_dims)),
28        ]
29
30    def _create_model(self):
31
32        hidden_layer_sizes = self._get_hidden_layer_sizes()
33        first_layer_size = hidden_layer_sizes[0]
34        n_dims = self.data.shape[1]
35
36        model = Sequential()
37
38        model.add(Dense(
39            first_layer_size,
40            input_dim= 2 * n_dims,
41            activation=self.hidden_activation,
42            W_regularizer=l1l2(self.l1_penalty, self.l2_penalty),
43            init=self.init))
44        model.add(Dropout(self.dropout_probability))
45
46        for layer_size in hidden_layer_sizes[1:]:
47            model.add(Dense(
48                layer_size,
49                activation=self.hidden_activation,
50                W_regularizer=l1l2(self.l1_penalty, self.l2_penalty),
51                init=self.init))
52            model.add(Dropout(self.dropout_probability))
53
54        model.add(Dense(
55            n_dims,
56            activation=self.output_activation,
57            W_regularizer=l1l2(self.l1_penalty, self.l2_penalty),
58            init=self.init))
59
60        loss_function = make_reconstruction_loss(n_dims)
61
62        model.compile(optimizer=self.optimizer, loss=loss_function)
63        return model
64
65    def fill(self, missing_mask):
66        self.data[missing_mask] = -1
67
68    def _create_missing_mask(self):
69        if self.data.dtype != "f" and self.data.dtype != "d":
70            self.data = self.data.astype(float)
71
72        return np.isnan(self.data)
73
74    def _train_epoch(self, model, missing_mask, batch_size):
75        input_with_mask = np.hstack([self.data, missing_mask])
76        n_samples = len(input_with_mask)
77        n_batches = int(np.ceil(n_samples / batch_size))
78        indices = np.arange(n_samples)
79        np.random.shuffle(indices)
80        X_shuffled = input_with_mask[indices]
81
82        for batch_idx in range(n_batches):
83            batch_start = batch_idx * batch_size
84            batch_end = (batch_idx + 1) * batch_size
85            batch_data = X_shuffled[batch_start:batch_end, :]
86            model.train_on_batch(batch_data, batch_data)
87        return model.predict(input_with_mask)
88
89    def train(self, batch_size=256, train_epochs=100):
90        missing_mask = self._create_missing_mask()
91        self.fill(missing_mask)
92        self.model = self._create_model()
93
94        observed_mask = ~missing_mask
95
96        for epoch in range(train_epochs):
97            X_pred = self._train_epoch(self.model, missing_mask, batch_size)
98            observed_mae = masked_mae(X_true=self.data,
99                                    X_pred=X_pred,
100                                    mask=observed_mask)
101            if epoch % 50 == 0:
102                print("observed mae:", observed_mae)
103
104            old_weight = (1.0 - self.recurrent_weight)
105            self.data[missing_mask] *= old_weight
106            pred_missing = X_pred[missing_mask]
107            self.data[missing_mask] += self.recurrent_weight * pred_missing
108        return self.data.copy()

Whew, that was a large chunk of code. The important part is updating our data where values are missing. We use some predefined weight along with the predictions of our NN to update only the missing value cells. Here is a diagram of our model:

The architecture of our Autoencoder

3. Evaluation

Let’s see how well our Autoencoder can impute missing data, shall we?

3.1 Preparing the data

We will use the encoding technique for our categorical data as discussed above. Let’s load (and drop a column with missing values from) our dataset.

1df = pd.read_csv("data/mushrooms.csv")
2df = df.drop(['sroot'], axis=1)

3.1.1 Making data dissapear

We will use MCAR as a driving process behind making missing data. Each data point in our dataset has 0.1 probability of being set to NaN.

1prob_missing = 0.1
2df_incomplete = df.copy()
3ix = [(row, col) for row in range(df.shape[0]) for col in range(df.shape[1])]
4for row, col in random.sample(ix, int(round(prob_missing * len(ix)))):
5    df_incomplete.iat[row, col] = np.nan

3.1.2 Encoding

Let’s one-hot encode our dataset using panda’s get_dummies and apply our missing data points accordingly:

1missing_encoded = pd.get_dummies(df_incomplete)
2
3for col in df.columns:
4    missing_cols = missing_encoded.columns.str.startswith(str(col) + "_")
5    missing_encoded.loc[df_incomplete[col].isnull(), missing_cols] = np.nan

3.2 Working out our Encoder (or just training it)

Finally, it is time to use our skillfully crafted model. We will train it for 300 epochs with a batch size of 256. All else is left to it’s default options.

1imputer = Autoencoder(missing_encoded.values)
2complete_encoded = imputer.train(train_epochs=300, batch_size=256)

1observed mae: 0.230737793827
2observed mae: 0.0371880909997
3observed mae: 0.0268712357369
4observed mae: 0.0232342579129
5observed mae: 0.0210763975367
6observed mae: 0.0191748421237

That’s all folks! Just kidding. The error seems to decrease so it might be wise to train for a few (or much more) epochs.

That run surprisingly fast on my 2.6 Ghz i7 (2013) with 16 Gb DDR3 ram. Should definitely try it out on a CUDA-enabled machine.

3.3 How well we did?

We have to do a little more housekeeping before answering that one. Here is an example of a row from our imputed dataset:

1complete_encoded[10, :10]

1array([  1.00000000e+00,   0.00000000e+00,   0.00000000e+00,
2         0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
3         0.00000000e+00,   1.00000000e+00,   4.18084731e-17,
4         5.83600606e-20])

Not what you expected? That’s all right. Let’s use maximum likelihood estimation (MLE) to pick winning prediction for each missing data point.

1def mle(row):
2    res = np.zeros(row.shape[0])
3    res[np.argmax(row)] = 1
4    return res
5
6col_classes = [len(df[c].unique()) for c in df.columns]
7
8dummy_df = pd.get_dummies(df)
9
10mle_complete = None
11
12for i, cnt in enumerate(col_classes):
13    start_idx = int(sum(col_classes[0:i]))
14    col_true = dummy_df.values[:, start_idx:start_idx+cnt]
15    col_completed = complete_encoded[:, start_idx:start_idx+cnt]
16    mle_completed = np.apply_along_axis(mle, axis=1, arr=col_completed)
17    if mle_complete is None:
18        mle_complete = mle_completed
19    else:
20        mle_complete = np.hstack([mle_complete, mle_completed])

Let’s see what we’ve got:

1mle_complete[10, :10]

1array([ 1.,  0.,  0.,  0.,  0.,  0.,  0.,  1.,  0.,  0.])

That’s more like it! Now we just have to reverse that get_dummies encoding…

1def reverse_dummy(df_dummies):
2    pos = defaultdict(list)
3    vals = defaultdict(list)
4
5    for i, c in enumerate(df_dummies.columns):
6        if "_" in c:
7            k, v = c.split("_", 1)
8            pos[k].append(i)
9            vals[k].append(v)
10        else:
11            pos["_"].append(i)
12
13    df = pd.DataFrame({k: pd.Categorical.from_codes(
14                              np.argmax(df_dummies.iloc[:, pos[k]].values, axis=1),
15                              vals[k])
16                      for k in vals})
17
18    df[df_dummies.columns[pos["_"]]] = df_dummies.iloc[:, pos["_"]]
19    return df
20
21rev_df = reverse_dummy(pd.DataFrame(data=mle_complete, columns=dummy_df.columns))
22rev_df = rev_df[list(df.columns)]

How much incorrect data points we have?

1incorrect = (rev_df != df)
2incorrect_cnts = incorrect.apply(pd.value_counts)
3incorrect_sum = incorrect_cnts.sum(axis=1)
4incorrect_sum[1]

13807.0

Whoops, that sounds like a lot. Maybe we didn’t do well overall? But how much are missing?

1missing = df_incomplete.apply(pd.isnull)
2missing_cnts = missing.apply(pd.value_counts)
3missing_sum = missing_cnts.sum(axis=1)
4missing_sum[1]

Whew, that is a lot, too! Okay, I’ll stop teasing you, here is the accuracy of our imputation:

1accuracy = 1.0 - (incorrect_sum[1] / missing_sum[1])
2print(accuracy)

10.786997146534

Roughly 79%. Not bad considering the amount of data we have. But we haven’t compared that to other approaches for data imputation (well, I have).

4. Conclusion(s)

And once again, the day is saved thanks to the powerp… the Autoencoder. It was quite fun and easy to build this model using Keras. Probably it will be even easier in the near future since Keras will be integrated directly into TensorFlow. Some questions that require further investigation remain unanswered:

Is this model effective for categorical data imputation?
Was our data highly correlated and easy to predict?
Can other models perform better? If so, when?
Can we incorporate uncertainty into our imputation? So we have a degree of belief of how good the imputed value is.

You can think about those questions. I am gonna go eat some mushrooms.

References

Keras - The library we used to build the Autoencoder
fancyimpute - Most of the Autoencoder code is taken from this awesome library
Autoencoders - Unsupervised Feature Learning and Deep Learning on Autoencoders
Denoising Autoencoders - Tutorial on Denoising Autoencoders with short review on Autoencoders
Data Imputation on Electronic Health Records - Great use of Deep Autoencoders to impute medical records data
Data Imputation using Autoencoders in Biology - Another great use of Autoencoders for imputation

Want to be a Machine Learning expert?

Join the weekly newsletter on Data Science, Deep Learning and Machine Learning in your inbox, curated by me! Chosen by 10,000+ Machine Learning practitioners. (There might be some exclusive content, too!)

You'll never get spam from me

Hacker's Guide to Neural Networks in JavaScript

Build Machine Learning models (especially Deep Neural Networks) that you can easily integrate with existing or new web apps. Think of your ReactJs, Vue, or Angular app enhanced with the power of Machine Learning models.

Get SH*T Done with PyTorch

Learn how to solve real-world problems with Deep Learning models (NLP, Computer Vision, and Time Series). Go from prototyping to deployment with PyTorch and Python!

Hacker's Guide to Machine Learning with Python

This book brings the fundamentals of Machine Learning to you, using tools and techniques used to solve real-world problems in Computer Vision, Natural Language Processing, and Time Series analysis. The skills taught in this book will lay the foundation for you to advance your journey to Machine Learning Mastery!

Hands-On Machine Learning from Scratch

This book will guide you on your journey to deeper Machine Learning understanding by developing algorithms in Python from scratch! Learn why and when Machine learning is the right tool for the job and how to improve low performing models!